„Dimensionen des Denkens“ skizziert die Geschichte der Logik über Aristoteles bis hin zu Gotthard Günthers mehrwertiger Logik. III. Die Seinsorte der Welt IV. Die proemiale Relation V. Polykontexturales Denken
Die proemiale Relation
Musst ins Breite dich entfalten,
Soll sich dir die Welt gestalten;
In die Tiefe musst du steigen,
Soll sich dir das Wesen zeigen.
Nur Beharrung führt zum Ziel,
Nur die Fülle führt zur Klarheit,
Und im Abgrund wohnt die Wahrheit.
Schiller
In die Breite entfaltet sich die mehrwertige Logik durch die Erweiterung der logischen Werte und Seinsorte. In die Tiefe steigt sie, indem sie zwischen Inhalt und Struktur unterscheidet. Die Polykontextural-Theorie von Gotthard Günther umfasst neben der mehrwertigen Logik auch die Kenogrammatik und Morphogrammatik. Um die (scheinbaren) Widersprüche des trans-klassischen Umtauschverhältnisses konsistent darzustellen und um die proemiale Relation zu erfassen, müssen wir uns mit Keno- und Morphogrammen befassen.
Kenogramme und Morphogramme
Die Morphogrammatik beschreibt die logische Ebene, die unterhalb der Wertbelegung von wahr und falsch liegt, unterhalb der Wertbelegung der klassischen Logik. Sie entfernt alle Inhalte und markiert nur Differenzen. Kenogramme markieren diese Differenzen, sie liegen noch vor der Belegung mit Werten. Der Name Kenogramm ist abgeleitet aus dem griechischen: kenos = leer. Kenogramm bedeutet „Leerzeichen“. Ein Morphogramm ist eine Folge von Kenogrammen. Einzelne Kenogramme können einmal oder mehrere Male in einem Morphogramm auftreten.
Die Morphogrammatik ist ein tieferliegender Formalismus, aus dem „auch das Letzte entfernt worden ist, was sich auf den kontingent-objektiven Charakter der Welt bezieht, nämlich der faktische Eigenschaften designierende logische Wert.“ (Gotthard Günther) Der designierende logische Wert wurde bisher beispielsweise mit „Subjekt“ belegt und die Negation mit „Objekt“. Die Morphogrammatik beschreibt die Struktur, in der die Differenz „Subjekt“ und „Objekt“ eingefügt werden kann, diese aber noch nicht voraussetzt. Dies gilt auch für die Differenz schön/hässlich, wahr/falsch, Geist/Materie…
Step by step: Die klassische Negationstafel wird wie folgt dargestellt:
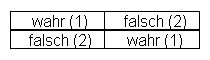
Entfernen wir die Wertbelegung wahr/falsch, bleiben lediglich zwei unterschiedliche Zeichen. Gotthard Günther hat hierfür einfache geometrische Symbole verwendet, ein Dreieck, Quadrat oder eine Raute: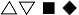 
Für 1-2 können wir 
oder 
schreiben. Das macht keinen Unterschied, weil die Kenogramme inhaltlich leer sind und somit für beliebige Inhalte stehen. Sie markieren die reine Differenz und bilden nur die Struktur ab. Wahr-falsch oder 1-2 ist strukturell identisch mit falsch-wahr oder 2-1. Deshalb kann die vertikale Wertefolge 1-2 und 2-1 kenogrammatisch so darstellt werden:
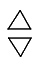
Eine Aussage p kann wahr (w) oder falsch (f) sein, eine zweite Aussage q kann ebenfalls wahr oder falsch sein. Für zwei Aussagen (p und q) ergeben sich vier Möglichkeiten der Wertbelegung:
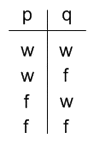
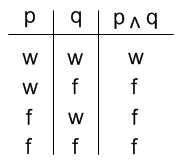
Wertefolgen sind in der klassischen Logik vierstellig. Eine Aussage p und eine Aussage q kann beispielsweise über eine Konjunktion (eine „UND-Verbindung“) miteinander verglichen werden. Zwei Aussagen werden miteinander verknüpft, indem man für jede mögliche Kombination ihrer Wahrheitswerte den Wert der Verknüpfung angibt. Eine Konjunktion ist nur wahr, wenn beide Aussagen wahr sind. Daraus ergibt sich folgende Wertefolge für die Konjunktion:
Insgesamt lassen sich 16 solcher Wertefolgen durch einfaches kombinieren bilden. Diese 16 Reihen entsprechen den 16 Wertefolgen (wie Tautologie, Adjunktion, Konjunktion, Disjunktion, Äquivalenz usw…) des Aussagenkalküls. Welche Wertefolgen das genau sind und was sie abbilden, ist an dieser Stelle nicht wichtig. Es genügt zu wissen, dass mit zwei Werten nicht mehr Kombinationen möglich sind.
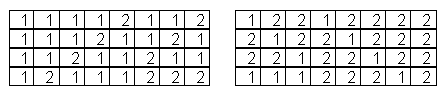
Die Spalten 9 -16 sind spiegelverkehrt zu den Spalten 8-1, sie sind die Negationen der Spalten 8-1. Die Wertefolge 1-1-1-1 (w-w-w-w) ist wiederum strukturell identisch mit der Wertefolge 2-2-2-2 (f-f-f-f). Werden diese Wertefolgen von ihren Inhalten entleert und kenogrammatisch dargestellt, ergibt sich folgendes Bild:
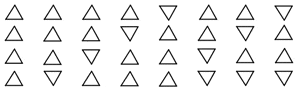
Trans-klassische Wertefolgen
Vom Ich zum Du gelangen wir über die Rejektion und für diese benötigen wir drei Werte. Bei der Rejektion wird die Alternative von 1 (Position, w) und 2 (Negation, f) als Ganzes verworfen und ein dritter Wert (3) wird gewählt. Die Rejektion, im Vergleich mit der Konjunktion:
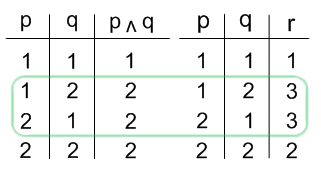
Die Rejektion (r) ist mit der Konjunktion (p ^ q) identisch, wenn keine Alternative angeboten wird, d. h. wenn die Werte von p und q identisch sind. Wird keine Alternative angeboten, kann auch nichts gewählt werden. Der angebotene Wert wird akzeptiert und damit wird implizit die zweiwertige Wahlalternative akzeptiert. Bieten p und q die Alternativ-Werte eines zweiwertigen Systems an (1 oder 2), dann kann die gesamte Alternative zurückgewiesen, bzw. rejiziert werden. Damit wird ein Wert gewählt (3), der nicht in das zweiwertige System gehört.
Um die Rejektion darzustellen benötigen wir ein drittes Kenogramm. In der mehrwertigen Logik stehen drei oder mehr Werte zur Verfügung. Die klassische vierstellige Wertefolge ermöglicht strukturell vier verschiedene Werte. Kombiniert man bei einer vierstelligen Wertefolge ein, zwei, drei oder vier Werte in allen möglichen strukturellen Variationen, erhält man 15 solcher Strukturen:
Die Reihe der Morphogramme zeigt, dass die Morphogramme 1-8 die klassische Belegung einer zweiwertigen Struktur darstellen. Eine trans-klassische Struktur wird erst dargestellt, wenn mehr als zwei Werte gewählt werden können. Die Wertefolge der Rejektion (1-3-3-2) wird im 11. Morphogramm dargestellt.
Um das Umtauschverhältnis von Ich und Du darzustellen, muss die Morphogrammatik nicht weiter vertieft werden. Wichtig an der bisherigen Darstellung ist, dass in der trans-klassischen Logik – im Gegensatz zur klassischen – ontologischer Ort und logischer Wert nicht identisch ist, Struktur und Inhalt werden getrennt.
Bisher haben wir uns mit dem Ergebnis der Verknüpfung von Aussagen befasst, beispielhaft mit der Konjunktion und Rejektion. Unhinterfragt bliebt der Prozess des Verknüpfens. Die Negation ist eine Operation, die den Übergang von einem Seinsort zum anderen beschreibt, also von A zu ¬ A. Auch bei diesem Übergang, dieser Operation sind ontologischer Ort und logischer Wert identisch. Die Morphogrammatik beschreibt auch die Struktur solcher Übergänge und damit die Struktur von Relationen. Mit der Morphogrammatik ist es möglich die proemiale Relation und das Umtauschverhältnis von Ich und Du darzustellen.
Die Struktur der Relation
Die Analyse der Gesprächssituation zeigte, dass das Umtauschverhältnis von Ich und Du eines der drei Umtauschverhältnisse bezüglich der Gesprächssituation ist. Als „Ich“ können wir jederzeit die Plätze wechseln mit einem „Du“. Die Analyse zeigte weiterhin, dass das trans-klassische Umtauschverhältnis nicht dem klassischen Umtauschverhältnis entspricht, weil ein einfaches Verhältnisglied (beispielsweise 1) mit einem komplexen Verhältnisglied (beispielsweise 2 und 3) getauscht wurde. Dies ist ein deutlicher Unterschied zum Umtauschverhältnis der klassischen Logik, bei dem beide Seiten symmetrisch sind. Kenogrammatisch lässt sich dieser „Widerspruch“ auflösen:
Eine Negation ist ein Umtauschverhältnis zwischen zwei Werten, d. h. ein gegenseitiger Austausch zweier Werte: A wird zu ¬ A. Die Rejektion kann nicht als ¬ (¬ A) geschrieben werden, denn dann würden sich die beiden Negationszeichen aufheben und A wäre das Ergebnis. Dies ist die Negation der klassischen Logik. Mit der trans-klassischen Negation hingegen wird keine „Sache“ negiert, sondern der Prozess des Verneinens, die Negation, wird negiert.
Die Negation ist in der klassischen Logik eine Relation. Eine Relation hat mindestens zwei Relationsglieder, die in einer Beziehung zueinander stehen. Bei
A ist die Negation von ¬ A
sind A und ¬ A die Relationsglieder (oder Relata) und „ist die Negation von“ bezeichnet die Beziehung, in der die Relationsglieder zueinander stehen:
A (Relatum) ist die Negation von (Relator) ¬ A (Relatum)
Relata und Relator bilden zusammen die Relation. Einfacher dargestellt:
R (x, y)
R steht für Relator (die Negation), x und y sind die Relata (A und ¬ A).
In der klassischen Umtauschrelation wechseln lediglich die beiden Relationsglieder (Relata) ihre Plätze:
R (y, x)
Die klassische Logik operiert nur mit Relationen, deren Relationsglieder ungeteilte Identitäten darstellen, gemäß dem Satz der Identität (Alles ist mit sich identisch und verschieden von anderem). Die trans-klassische Logik betrachtet tiefergehend die Beziehung des Relators hinsichtlich seiner Relata. Sie untersucht die Struktur einer Relation, vergleichbar mit den Morphogrammen, die die Struktur der Wertefolgen abbilden.
Komplexitätsgrade von Relator und Relata
Ein Relator und ein Relationsglied stehen in einem Ordnungsverhältnis zueinander, bei dem der Relator höherrangig, von höherer logischer Ordnung ist, als das Relationsglied. In der trans-klassischen Logik kann ein Relator mit einem Relatum getauscht werden. Das Umtauschverhältnis der trans-klassischen Logik ist kein Wechsel auf einer Ebene, wie etwa R (x, y) in R (y, x) überführt werden kann.
Im trans-klassischen Umtauschverhältnis bedeutet ein Umtausch von Relata und Relator immer auch eine Zu- oder Abnahme des Komplexitätsgrades der Relatoren bzw. der Relata.
„Der Relator kann zum Relatum werden, doch nicht in der Relation, für die er zuvor die Beziehung einrichtete, sondern nur relativ zu einem Verhältnis bzw. Relator höherer Ordnung.„
(Gotthard Günther)
Ein Umtausch, der ein Relatum in einen Relator transformiert (Zunahme), macht dieses Relatum zu einem Relator hinsichtlich Relata von niederer Ordnung. Ebenso wird aus einem Relator ein Relatum (Abnahme) in Bezug auf einen Relator höherer Ordnung.
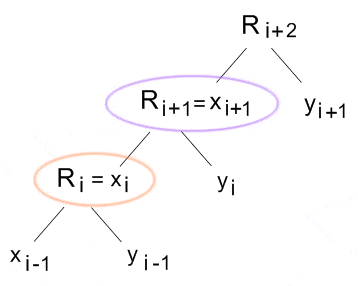
Für eine gegebene Relation (der Index i steht für eine höhere bzw. niedrigere logische Ordnung.)
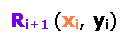
gilt: Wird das Relatum x oder y zum Relator, erhalten wir:
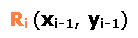
Hier ist Ri = xi oder yi. Wird der Relator zu einem Relatum erhalten wir:
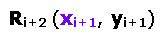
Hier ist Ri+1 = xi+1 oder yi+1.
Das proemiale Verhältnis
Die Verbindung zwischen Relator und Relata nennt Gotthard Günther das proemiale Verhältnis, da es der symmetrischen Umtauschrelation und der Ordnungsrelation vorangeht und deren gemeinsame Grundlage bildet. Das proemiale Verhältnis stellt eine tiefere Fundierung der Logik bereit, aus dem die klassischen Relationen (Umtausch- und Ordnungsrelation) hervorgehen.
Das Proemialverhältnis konstituiert jede Relation als solche. Damit ist es die Basis, auf der sich Umtausch- und Ordnungsrelation vollziehen kann. Das Proemialverhältnis wird von der Proemialrelation geregelt. Sie überführt Relata in Relatoren und umgekehrt. Dies jedoch nicht innerhalb einer Relation, sondern zwischen Ebenen höherer und niedrigerer logischer Komplexität. Die Proemialrelation gehört zur Ebene der kenogrammatischen Strukturen, die vor der Belegung mit Werten liegt und eine reine Möglichkeit darstellt.
Das Proemialverhältnis definiert den Unterschied zwischen Unterscheidung und Unterschiedenem, was das gleiche ist wie zwischen Relata und Relator. Gemeinsam hat sie mit der klassischen Umtauschrelation: ein Relator kann zum Relatum werden. Ein Willenssystem kann zum Erkenntnissystem werden, das „Ich“ kann im Gespräch zum „Du“ werden.
Die Proemialrelation entfaltet die strukturellen Eigenschaften eines Umtauschs, aber dieser Umtausch ist kein symmetrischer. Wird ein Relator mit einem Relatum getauscht, ist dies ein Umtausch zwischen niederer und höherer logischer Ordnung. Damit sind Relata keine ungeteilten Identitäten mehr, das „Subjekt“ kann sowohl Relatum, als auch Relator sein.
Wir können einen Gesprächspartner als Relation zwischen seinen Körperzellen betrachten, wobei die Körperzellen hierbei die Relata sind. Wir können einen Gesprächspartner jedoch auch als Relatum in einer komplexeren Ordnung darstellen, in einem Gespräch. Ein „Ich“ kann beides sein: ein Relator relativ zu seinen Körperzellen und ein Relatum innerhalb der umfassenderen Relation eines Gesprächs.
Die Proemialrelation repräsentiert das Ineinandergreifen von Umtausch und Ordnung. Das Verhältnis zwischen Relator und Relatum ist sowohl durch Umtausch, als auch durch Ordnung strukturiert. Es ist ein Umtausch zwischen niederer und höherer logischer Ordnung, also ein Umtauschverhältnis auf der Basis einer Ordnung, oder ein Ordnungsverhältnis unter der Voraussetzung eines Umtauschs – ein Zusammenspiel von Hierarchie und Heterarchie.
 |
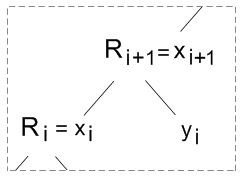kenogrammatisch dargestellt: |  |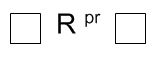
Rpr ist der Relator der Proemialrelation, die Kenogramme 
und sind die Relata. Die Kenogramme können so ausgefüllt werden, dass eine aktuelle Wertbelegung entweder eine symmetrische Umtauschrelation repräsentiert (xi wird mit yi getauscht) oder eine nicht-symmetrische Ordnungsrelation (Ri wird mit xi getauscht, der Relator wird zum Relatum).
Die Struktur der Proemialrelation ist eine Umtauschrelation:
Rpr
Die Proemialrelation beschreibt, dass ein Relator von höherer logischer Ordnung ist, als die Relata, und dass die Relata auf derselben logischen Ebenen liegen. Sie beschreibt weiterhin, dass wenn wir Relata und Relator tauschen (was möglich ist), wir dies nicht innerhalb derselben logischen Ebene tun können, sondern nur, indem die logische Ebene zu- oder abnimmt (i+1 oder i-1). Ri+1 und xi+1 stehen in einem Umtauschverhältnis zueinander, doch xi+1 ist ein Relatum einer Relation Ri+2 und Ri+1 ist der Relator zu den Relata xi und yi.
|
Rpr | |
| A | ist das Gegenteil von | ¬ A |
| Relator | ist von höherer logischer Ordnung als | Relata |
| Mensch | kann mehr Komplexität verarbeiten als | Ameise |
| Umtauschverhältnis | ist die Negation von | Ordnungsverhältnis |
| 1 ↔ 2 | wird zurückgewiesen zu | 3 |
| 3 | ist die Rejektion von | 1 ↔ 2 |
| Anton | liebt | Berta |
| Anton | ist verheiratet mit | Berta |
| A | ist identisch mit | A |
Zusammengefasst:
- Das proemiale Verhältnis besagt, dass der Relator von höherer logischer Ordnung ist, als die Relata.
- Die proemiale Relation erlaubt einen Umtausch von Relator und Relata.
- Aus dem proemialen Verhältnis folgt, dass dies nur in Bezug auf unterschiedliche logische Ebenen, in Bezug auf verschiedene Relationen möglich ist.
„Was die Proemialrelation einführt, ist eine heterarchische Verbindung zwischen Form und Stoff und folglich zwischen Subjekt und Objekt und deshalb auch zwischen Wollen und Erkennen.„
Gotthard Günther
Nächstes Kapitel: V. Polykontexturales Denken
