Seitdem sich der Mensch mit Logik beschäftigt, sie erforscht, sieht er sich mit Paradoxien bzw. Antinomien konfrontiert. Logiker und Philosophen sind in der Regel über diese Phänomene recht beunruhigt, da anscheinend widerspruchsfreie Denkvorgänge zu widersprüchlichen Ergebnissen führen (können).
Einleitung
Diese Ausarbeitung beansprucht nicht eine mathematische Abhandlung zu sein. D. h. ich beabsichtige nicht und sehe mich auch außerstande, die mathematische Logik und ihre Beweise in Bezug auf die Antinomien hier en detail vorzuführen. Dennoch halte ich es nicht nur für möglich, sondern auch für unverzichtbar, die Voraussetzungen, die Grundannahmen und die Resultate der mathematischen Logik von außerhalb derselben zu betrachten, eben aus philosophischer Sicht. „Die Philosophie prüft nicht die Kalküle der Mathematik, sondern nur, was die Mathematiker über die Kalküle sagen.“ (Wittgenstein, Ludwig; Philosophische Grammatik; 2. Aufl. Frankfurt a.M. 1978, S. 396)
Meine Darstellungen stützen sich fast ausschließlich auf eine Abhandlung von Norbert Domeisen1, deren thematischer Schwerpunkt die Kritik am Unvollständigkeitsbeweis von Kurt Gödel aus dem Jahre 1931 ist. Obwohl das Unvollständigkeitstheorem ebenfalls der Sache nach zum Thema dieser Ausarbeitung gehört, habe ich es ausgespart, weil ich dazu eigens eine weitere Arbeit anschließen werde.
Begriffsklärung
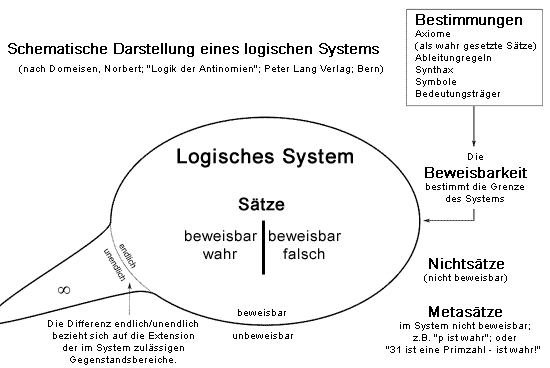
In der Frage danach, wie Antinomien zustande kommen und wie sie darzustellen sind, muss unser Augenmerk besonders auf die sprachliche Konzeption der Logik gerichtet werden. Denn das Zutage treten von Widersprüchen und Antinomien kann letztlich nicht auf die Symbole der Logik zurückgeführt werden, sondern muss in den Konstruktionen aufgespürt werden, die aus den Begriffs- und Symboldefinitionen resultieren. „Und die Symbolik kann nicht präziser, nur einfacher und kürzer sein, als die sprachliche Umschreibung, für die sie als Abkürzung steht. Sie ist insbesondere nicht davor gefeit, sprachliche oder gedankliche Mehrdeutigkeiten zu übernehmen und diesen den Schein von Eindeutigkeit und vollkommener Klarheit zu geben.“ (S. 119)1 Daher werden im Folgenden wichtige Schlüsselbegriffe der Logik charakterisiert, um die allgemeinen Verhältnisse in logischen Systemen aufzuzeigen. Daran anschließend habe ich einige dieser Relationen in einem Diagramm dargestellt.
Wahrheit: In der Metasprachlichen Perspektive bezieht Wahrheit sich auf die Übereinstimmung zwischen einer Aussage und dem Objekt dieser Aussage. Innerhalb eines logischen Systems kann die Wahrheit eines Satzes nur auf die (gesetzte) Wahrheit der Axiome zurückgeführt werden.
Satz: ist eine wahrheitsdefinite Aussage in einem Axiomensystem. Ein Satz oder dessen Negation muss sich aus den Axiomen des Systems ableiten lassen. Die Wahrheit einer Aussage p beruht daher auf der Wahrheit der Axiome. Lässt sich weder p noch ¬p ableiten, ist p kein Satz des Systems. „Wenn hier also von Sätzen die Rede ist, sind damit Aussagen in axiomatischen Systemen gemeint. Und eine solche Aussage kann, mit Tarski zu reden, >>nun einfach als eine Aussagefunktion definiert werden, die keine freie Variable hat<<„. (S. 51)1
Axiom: Als wahr gesetzter Satz des Systems. Axiome und Ableitungsregeln definieren die Grenzen des Systems, sie stecken seinen Anwendungsbereich ab. Insofern ist jedes axiomatische System vollständig. Gelingt es sowohl p als auch ¬p abzuleiten, ist das System widersprüchlich, d. h. die Axiome stehen in einem Widerspruch zueinander. Ein Axiomensystem hat widerspruchsfrei, unabhängig, hinreichend und notwendig zu sein (S.36 Fußnote 54)1.
Nichtsatz: Symbolfolge für die keine Ableitung (d. h. Beweis) existiert (oder gefunden wurde). Ein Nichtsatz ist nicht wahrheitsdefinit. (z. B.: „+:4 = 25″; „p ∧∨ q“; „kein Dies Satz. ist“)
Metasatz: ist eine Aussage über einen Satz oder Nichtsatz des Systems. „Meatsätze sind nie Sätze des Systems, sondern immer Metasätze über Sätze oder Nichtsätze des Systems“ (S. 54)1. Daraus folgt, dass die Wahrheit von Metasätzen sich stets auf die Entscheidbarkeit ihrer Objektsätze gründet, denn der Metasatz “ p ist wahr“ ist falsch, wenn p beweisbar falsch ist, und er ist eine Vermutung, wenn weder für p noch für ¬p eine Ableitung vorliegt. Beispiele für Metasätze: “ p ist wahr“; “ p ist falsch“; “ x ist weder wahr noch falsch“
Behauptung: Aussage, deren Wahrheit vorausgesetzt, aber (noch) nicht bewiesen ist. Gelingt der Beweis, wird die Behauptung zu einem wahren, und deren Negation zu einem falschen Satz des Systems.
Negation: Die Negation kehrt den Wahrheitswert eines Satzes um. Wenn p wahr ist, dann muss ¬p falsch sein, und umgekehrt. (Eine negierte Aussage ist nicht das Gegenteil einer Behauptung, sondern die Behauptung des Gegenteils.) „Die Annahme, ein widerspruchsfreies Axiomensystem lasse nur den Beweis inhaltlich wahrer Aussagen zu, ist, sobald ein solches System die Negation miteinbezieht, falsch.“ (S. 117)1.
Beweisbarkeit: Über die Beweisbarkeit entscheidet das gelingende Verfahren, in dem die Wahrheit oder Falschheit eines Satzes aus den Axiomen mittels der Ableitungsregeln ermittelt wird. Dies impliziert die Endlichkeit und das faktische Vorliegen eines Beweises (d. h. einer Ableitungskette). Hieraus folgt, dass die Behauptung, Sätze könnten wahr sein, ohne dass ein Beweis vorliegt, die logische Bedingung für Wahrheit/Falschheit negiert. Sätze können beweisbar wahr oder beweisbar falsch sein. Liegt keiner der beiden Beweise vor, ist also ein Satz nicht beweisbar, kann er nicht zum System gerechnet werden. „Es gibt, so betrachtet, nur ein Beweisverfahren für die Wahrheit. Der Beweis für Falschheit ist der Beweis der Wahrheit der Negation.“ (S. 109)1 „Der Beweis hat eben nicht nur den Zweck, die Wahrheit eines Satzes über jeden Zweifel zu erheben, sondern auch den, eine Einsicht in die Abhängigkeit der Wahrheit von einer anderen zu gewähren.“ (Frege, Gottlob; Die Grundlagen der Arithmetik, Stuttgart 1987; S. 26).
Entscheidbarkeit: Kann für einen Satz in einem endlichen Verfahren angegeben werden, ob er wahr oder falsch ist, so ist dieser Satz entscheidbar. Unentscheidbar kann ein Satz sein, wenn a) er nicht entsprechend den Regeln für Sätze formuliert (sprich im System sinnlos) ist, wenn b) sowohl für den Satz als auch für seine Negation eine Ableitung vorliegt (d. h. dass das System Widersprüche enthält), wenn c) bislang weder für den Satz, noch für seine Negation eine Ableitung gefunden werden konnte, und d) wenn es sich bei dem Satz um eine nicht aus den Axiomen ableitbare Allquantifikation (oder negierte Existenzquantifikation) über einen unendlichen Gegenstandsbereich handelt. Fall d) würde ein unendliches Induktionsverfahren als Beweis für den Satz (oder seine Negation) erfordern. Die letzte Möglichkeit stellt die Widerlegung der Negation des Satzes dar: die Widerlegung des Satzes ∀xF(x) erfolgt durch den Beweis für seine Negation ¬∀xE(x) bzw. ∃x¬E(x). Kann kein x gefunden werden, dass die Existenzbehauptung wahr macht, stehen wir in dem Versuch der Widerlegung vor Fall c).
Vollständigkeit: Die Axiome konstituieren den Umfang des Systems. Aus ihnen müssen alle entscheidbaren Sätze ableitbar sein. Wenn alle Sätze eines Systems entscheidbar sind, ist es vollständig. Vollständigkeit ist eine Implikation der Forderung nach Widerspruchsfreiheit, denn wenn von einem Satz sowohl festgestellt werden kann, dass er wahr, als auch, dass er falsch ist, wird das System, d. h. die Menge der Sätze des Systems entgrenzt [denn aus einem Widerspruch lässt sich alles ableiten: (A ∧ ¬A) → B ]. Der Begriff der Vollständigkeit könnte hier nicht mehr greifen.
Widerspruchsfreiheit: Widerspruchsfreiheit liegt vor, wenn sich aus den Axiomen keine Sätze ableiten lassen, die zugleich mit ihrer Negation wahr sind. Die Widerspruchsfreiheit eines Axiomensystems ist hinreichend zur Erfüllung der Forderungen nach Entscheidbarkeit und Vollständigkeit. Denn vollständig ist ein System, wenn alle Sätze des Systems entscheidbar sind, und entscheidbar ist ein System, wenn von jedem seiner Sätze gilt, dass p ∨ ¬p oder ¬(p ∧ ¬p), was logisch äquivalent ist. „Wenn diese Überlegungen richtig sind, dann bleibt als einzige Anforderung die Widerspruchsfreiheit. Denn der Nachweis der Widersprüchlichkeit ist dann durch den Nachweis eines unentscheidbaren Satzes erbracht, der seinerseits die Unvollständigkeit beweist.“ (S. 120)1
Im System gibt es keinen Beweis für die Widerspruchsfreiheit, denn a) das System müsste ein entsprechendes Prädikat für die Widerspruchsfreiheit zur Verfügung haben, woraus nur Tautologien resultierten, b) und im Falle eines unendlichen Systems wäre dieser Beweis gleichbedeutend mit der Verifikation einer Allaussage: ∀xE(x) [x = ein beliebiger Satz; E(x) = (x ist ein entscheidbarer Satz)].
„Nur wenn alle Sätze entscheidbar sind, ist das System vollständig, dann aber gibt es auch keine Sätze, die unentscheidbar sind, weil sie Gegenteiliges behaupten und damit zugleich widersprüchlich sind. Dieser Zusammenhang zeigt, dass die Widerspruchsfreiheit eine Anforderung ist, die genau dann erfüllt ist, wenn es keine unentscheidbaren Sätze gibt.“ (S. 111)1
Antinomien
Die charakteristischen Merkmale von Antinomien sind Widersprüchlichkeit, Selbstbezüglichkeit und Zirkularität. Eine Antinomie wird semantisch genannt, wenn sie aus der Bezugnahme auf die Bedeutung der verwendeten Symbole hervorgeht. Sie wird syntaktisch genannt, wenn die sie kennzeichnenden Widersprüche aus den formalen, strukturellen Zusammenhängen hervorgehen.
Der Barbier
In einem Dorf gibt es einen Barbier, der alle im Dorf rasiert, die sich nicht selbst rasieren. Nun stellt sich die Frage, ob der Barbier sich selbst rasiert oder nicht. Rasiert er sich nicht selbst, müsste er, weil er dann zu denen gehörte, die sich nicht selbst rasieren, sich rasieren. Daraus folgt aber wiederum, dass er sich nicht rasieren dürfte. Diese paradoxe Situation resultiert aus der Doppeldefinition des Begriffs Barbier: 1) der, der alle Dorfbewohner rasiert, die sich nicht selbst rasieren; b) ein Dorfbewohner.

Das Lügnerparadox
Varianten:
- „Epimenides, der Kreter, sagte, alle Kreter wären Lügner und alle sonst von Kretern aufgestellten Behauptungen wären gewiss Lügen.“
Mit x [eine beliebige Aussage] und K(x) [ein Kreter macht eine Aussage x] kann die Aussage A von Epimenides wie folgt formuliert werden: A ≡ ∀x (K(x) → ¬x) Setzt man in diese Allaussage für x die Aussage A selbst ein, so erhalten wir: K(A) → ¬A (vgl. S. 325ff)2.
Dies besagt nun, dass aus der Annahme „A ist wahr“ der Schluss „A ist falsch“ gezogen wurde.
- „Ich lüge.“ (bzw. „Ich sage die Unwahrheit über etwas„) oder „Dieser Satz ist falsch.“ Beide Sätze haben kein logisches Subjekt, denn das, wofür hier etwas und dieser stehen, kann durch die Selbstbezüglichkeit der Sätze nicht bestimmt werden.
Das Mengenparadox
Die Bildung der Menge aller Mengen impliziert, dass die Menge aller Mengen sich selbst enthalten muss, denn sonst wäre sie nicht die Menge aller Mengen. Enthält sie sich selbst, wird die Definition der Menge aller Mengen in gewisser Weise zirkulär. Um diese Problematik zu umgehen, ersann man den Begriff der normalen Menge, die sich nicht selbst enthält R = {M | ¬ (M ∈ M)}, und den der nicht-normalen Menge, die sich selbst enthält {M | M ∈ M}. Nun lässt sich weiterfragen, ob die Menge aller normalen Mengen R selbst normal sei oder nicht. Aus der Annahme, R sei nicht normal (R ∈ R), folgt, dass R selbst zu den normalen Mengen gehört. Umgekehrt folgt aus der Annahme, R sei normal (¬(R ∈ R)), dass R selbst nicht zu den normalen Mengen gehört.
Zur Auflösung dieser Antinomie kann Russels Typentheorie herangezogen werden, welche u. a. besagt, dass die Definition einer Menge niemals die Gesamtheit der zu definierenden Menge voraussetzen darf, sprich eine Mengendefinition darf nicht zirkulär sein. Das bedeutet, „dass eine Klasse niemals Argument der sie definierenden Funktion sein kann.“ (S. 79)1. In der obigen Definition {M | ¬(M ∈ M)} wird M als gegeben vorausgesetzt, obwohl M zunächst durch die Zuordnungsregel konstituiert werden muss. Ausdrücke wie x ∈ x oder ¬ (x ∈ x) nennt man nicht-prädikative oder imprädikative Ausdrücke. Eine Definition ist imprädikativ, wenn sie Bezug nimmt auf eine Gesamtheit, zu der auch das zu Definierende gehört. Somit enthält ein imprädikativer Ausdruck kein wirkliches Prädikat, da die Bedeutung des Prädikates sich nur aus sich selbst erklärt und daher leer bleibt. Für gewöhnlich sind Prädikate in ihrer Bedeutung unabhängig vom Kontext, in dem sie verwendet werden. Das Prädikat „ist rot“ beispielsweise meint eine Zuweisung einer bestimmten Farbe und seine Bedeutung hängt in keiner Weise vom Gegenstand ab, dem das Prädikat zu- oder abgesprochen wird.
„Russel schloss sich dieser Analyse an und untermauerte seine 1903 gegebene Analyse von Aussageformen wie „x∈ x„, die sich ihm als sinnlos ergeben hatten, durch die Feststellung, dass diese illegitimen Ausdrücke gerade die im Poincaréschen Sinne nicht-prädikativen (oder „imprädikativen“) Ausdrücke seien.“ (S. 324)2
Cantors Diagonalargument
Mit folgendem Verfahren beabsichtigte Georg Cantor (1845-1918) zu zeigen, dass die Menge der reellen Zahlen zwar unendlich, jedoch nicht abzählbar sei. Er beschränkte sich für den Nachweis auf das Intervall zwischen 0 und 1:
Gegeben sei eine vollständige unendliche Liste aller Reellen Zahlen, mit unendlich vielen Nachkommastellen, zwischen 0 und 1 (offenes Intervall ]0,1[). Aus dieser Liste lässt sich wie folgt eine weitere Zahl konstruieren, die in der Liste nicht mit aufgeführt ist: Die neue Zahl beginnt ebenfalls mit „0,“ Man wähle die erste Ziffer der ersten Dezimalstelle der neuen Zahl um 1 verschieden von der ersten Ziffer (nach dem Komma) der ersten Zahl in der Liste, die zweite Ziffer der neuen Zahl um 1 verschieden von der zweiten Ziffer der zweiten Zahl in der Liste usw. Formal ausgedrückt: Die n-te Ziffer der neuen Zahl sei mit z (n-te Ziffer der n-ten Zahl aus der Liste) z + 1 (und bei z = 9 sei sie 0). Die resultierende Zahl unterscheidet sich von jeder Zahl in der Liste durch mindestens eine Ziffer. Dennoch gehört sie in das offene Intervall ]0,1[. Dieser Vorgang lässt sich beliebig oft wiederholen.
|
Ziffer 1
|
Ziffer 2
|
Ziffer 3
|
Ziffer 4
|
…
|
||
|
Zahl 1
|
0,
|
0
|
0
|
0
|
0
|
|
|
Zahl 2
|
0,
|
0
|
0
|
0
|
1
|
|
|
Zahl 3
|
0,
|
0
|
0
|
1
|
2
|
|
|
Zahl 4
|
0,
|
0
|
2
|
1
|
6
|
|
|
…
|
…
|
|||||
|
konstruierte
Zahl
|
0,
|
1
|
1
|
2
|
7
|
…
|
Aus der Annahme der Vollständigkeit der Liste der reellen Zahlen in einem Intervall resultiert somit die Folgerung der Unvollständigkeit der Liste. Dieser Widerspruch offenbart die antinomische Struktur dieses Arguments. Die Prämisse, dass die Liste vollständig sei, ist keinesfalls unstrittig. Sie bedarf einer genaueren Betrachtung bzw. einer Begründung. „Cantors Diagonalargument setzt nun aber, … , voraus, was zuerst bewiesen werden müsste, damit es stichhaltig wäre, nämlich, dass es überhaupt möglich ist, in einem unendlichstelligen Zahlenquadrat alle Dezimalbruchzahlenvariationen unterzubringen.“ (S. 65)1
Untersuchen wir dazu zunächst die Gegebenheiten in endlichen Listen. Hierfür macht es keinen Unterschied, ob wir Listen von Dezimalbrüchen oder Listen natürlicher Zahlen betrachten, denn in Cantors Liste bleibt die Ziffer vor dem Komma unverändert.
Das Diagonalargument setzt zur Konstruktion einer Diagonalen ein Zahlenquadrat voraus. In einem Quadrat mit n Zahlen müssen demnach alle Zahlen n Stellen haben (bzw. die n-te Zahl muss mindestens n Ziffern haben). Die einzelnen Ziffern jeder Zahl können zwischen 10 Ziffern (0-9) variieren. Die Anzahl der Variationsmöglichkeiten bei n-stelligen Zahlen beträgt somit 10n. Eine endliche, für das Diagonalargument geeignete Liste enthält somit n Zahlen mit n Stellen. Beispielsweise umfasst eine Liste mit dreistelligen Zahlen (n = 3) nur 3 Zahlen. Mögliche Variationen gibt es jedoch 103 = 1000. Allgemein formuliert: Eine endliche Liste mit n-stelligen Zahlen umfasst stets nur n von 10n möglichen Zahlen.
Wir definieren eine endliche Liste von Zahlen, indem wir ihr bestimmte Zahlen zuordnen. Die Vollständigkeit einer Liste kann hier zweierlei bedeuten:
- Die Liste ist definitionsgemäß vollständig, d. h. sie enthält all jene Zahlen, die ihr definitionsgemäß zugeschrieben werden. Jede durch das Diagonalargument konstruierte Zahl ist nicht in dieser Liste enthalten, was jedoch keinen Einfluss auf ihre Vollständigkeit hat, welche durch die Listendefinition gegeben ist.
- Im Sinne der Variationsmöglichkeiten (10n) ist die Liste unvollständig, denn ihr fehlen stets 10n – n Zahlen. Fügten wir der Listen alle fehlenden Zahlen hinzu, machten wir sie also in diesem Sinne vollständig, wäre das Diagonalargument nicht mehr anwendbar, denn wir erhielten kein Zahlenquadrat.
Für endliche Zahlenlisten gilt also: Im 1. Fall ist die Anwendung des Diagonalarguments trivial, im 2. Fall ist das Diagonalargument nicht anwendbar.
Nun setzt aber Cantor für sein Verfahren a) die Vollständigkeit (im Sinne beider! soeben genannten Interpretationen) der Liste und b) die Anwendbarkeit des Diagonalarguments voraus. a) besagt, dass die Liste alle reellen Zahlen zwischen 0 und 1 enthält, b) besagt, dass diese Liste ein Zahlenquadrat ist. Beide Voraussetzungen münden in der Behauptung, dass n = 10n gelte. In endlichen Listen stellt diese Aussage ein Widerspruch dar. Die Gültigkeit der Behauptung n = 10n für unendliche Listen (bzw. für n → ∞) bedarf eines Beweises, von dessen Gelingen die Gültigkeit des Diagonalarguments abhängt. Unterscheiden wir die zwei möglichen Fälle:
- Der Beweis gelingt nicht (d. h. der Beweis für ¬ (n = 10n) für n → ∞ gelingt). Folglich erhalten wir kein Zahlenquadrat und können das Diagonalargument nicht zur Anwendung bringen.
- Der Beweis gelingt. Folglich ist die Liste vollständig. D. h. der Beweis für n = 10n (mit n → ∞) ist zugleich der Beweis für die Vollständigkeit der Liste. Folgt nun aber aus der bewiesenen Vollständigkeit der Liste nach Cantor die Unvollständigkeit derselben, sehen wir uns mit einem Widerspruch konfrontiert. Das Verfahren, welches diesen Widerspruch hervorbringt, kann seinerseits nicht als ein zulässiges Beweisverfahren (für welche Behauptung auch immer) gelten.
Wir haben die Stichhaltigkeit des Diagonalverfahrens, als Beweis für die Nichtabzählbarkeit der Menge der reellen Zahlen, auf das Gelingen des Beweises für die Behauptung n = 10n (mit n →∞) zurückgeführt. Jedoch zeigt sich an der obigen Fallunterscheidung, dass das Diagonalargument entweder unanwendbar (1) oder obsolet (2) ist. Warum obsolet? Weil man, solange man akzeptiert, dass die Vollständigkeit als bewiesen gilt, nicht zugleich annehmen kann, das Gegenteil, also die Unvollständigkeit, sei ebenfalls beweisbar. Der Beweis für die Vollständigkeit ist zugleich der Beweis dafür, dass die Behauptung, die Liste sei unvollständig, falsch ist. „Denn ein Beweis dafür, dass unendliche Zahlenquadrate im Gegensatz zu endlichen alle Variationsmöglichkeiten von n-stelligen Zahlen umfassen und damit vollständig wären, wäre implizit auch der Beweis für die Nichtanwendbarkeit des Diagonalargumentes auf sie.“ (S. 64)1 Cantors widersprüchliches Ergebnis muss demnach als Indiz auf die Fehlerhaftigkeit des Beweisverfahrens und/oder seiner Prämissen betrachtet werden. Eine wesentliche Fehlannahme besteht darin, dass das Unendliche mit Mitteln angegangen wird, welche für den Umgang mit dem Endlichen bestimmt sind. Es ist etwas anderes eine endliche Liste von Zahlen vor sich zu haben, als sich eine unendliche Liste als gegeben vorzustellen. „Nur muss man sich durchaus vor der Vorstellung hüten, dass, wenn eine unendliche Menge definiert ist, man nicht bloß die für ihre Elemente charakteristische Eigenschaft kenne, sondern diese Elemente selbst sozusagen ausgebreitet vor sich liegen habe und man sie nur der Reihe nach durchzugehen brauche, … , ob in der Menge ein Element von dieser oder jener Art existiere.“ (Weyl, Hermann; Über die neue Grundlagenkrise der Mathematik 1921; In: Becker, Oskar; Grundlagen der Mathematik, Frankfurt a.M. 1975, S. 337)
„(…) Cantor [geht] in Bezug auf unendliche Größen in der Mathematik und Mengenlehre demnach recht unkritisch vor, indem er Eigenschaften des Unendlichen voraussetzt, die er zuerst beweisen müsste und dann mittels seines Diagonalverfahrens diese Voraussetzung widerlegt, daraus aber nicht den Schluss zieht, dass demnach die Voraussetzung falsch ist, sondern umgekehrt, daraus folgert, das Unendliche, konkret die unendliche Reihe der natürlichen Zahlen sei noch zu überbieten durch noch größere Zahlen, nämlich die von ihm so genannten transfiniten Kardinalzahlen.“ (S. 67)1
Meine Stellungnahme zum Diagonalverfahren
Ich stimme mit Cantors Behauptung, dass die Menge der reellen Zahlen (in einem beliebigen Intervall) nicht-abzählbar unendlich sei, überein, trotzdem ich seine Prämisse, eine Liste von reellen Zahlen könne als vollständig gegeben angenommen werden, für falsch halte. Neben den oben dafür angeführten Gründen spricht folgender Ansatz gegen seine Prämisse:
Die Vorstellung von einer vollständigen Liste aller reellen Zahlen im Intervall ]0,1[ impliziert z. B. die Möglichkeit, die erste reelle Zahl r zu benennen, für die gilt r > 0, denn auch diese Zahl muss in der vollständigen Liste enthalten sein. Abgesehen davon, dass die Benennung von r praktisch unmöglich ist, kann das Auffinden von r auch als prinzipiell unmöglich nachgewiesen werden. Widerspruchsbeweis: Angenommen r sei die erste reelle Zahl, welche die Bedingung r > 0 erfüllt, d. h. r sei die erste positive reelle Zahl nach 0. Mit x > 0 gilt ebenso, dass x/2 > 0, sowie auch x > x/2. Für x setzen wir r ein: r > 0 ⇒ r/2 > 0 ⇒ r > r/2. Nun besagt aber r > r/2, dass r/2 der 0 näher steht als r, womit die Eingangsbehauptung widerlegt wäre.
Da diese Argumentation von jeder konkreten reellen Zahl abstrahiert, zeigt sie auf, dass es keine erste positive reelle Zahl nach 0 geben kann, bzw. dass diese unter keinen Umständen als Zahl darstellbar ist. Daher kann auch davon abgesehen werden, dass es prinzipiell möglich sei, eine vollständige Liste aller reellen Zahlen in einem Intervall aufzustellen, womit eine notwendige Bedingung für das Diagonalverfahren hinfällig wird. Dennoch bestätigt meine Argumentation Cantors Behauptung der Nichtabzählbarkeit der reellen Zahlen. Denn eine beliebige unendliche Liste reeller Zahlen r0, r1, r2, … , rn (mit n → ∞) kann, wie oben gezeigt, immer erweitert werden durch die reellen Zahlen r0/2, r1/2, r2/2, … , rn/2 (mit n → ∞). Desweiteren muss die Anzahl der Zahlenreihen, durch die eine gegebene Liste erweitert werden kann, als unendlich angesehen werden, da der Nenner 2 im obigen Beispiel durch jede beliebige positive natürliche Zahl m > 0 ersetzt werden kann: r0/m, r1/m, r2/m, … , rn/m. Welche Einteilung für das Intervall auch immer gewählt wird, sie wird keine vollständige Darstellung des Intervalls hervorbringen. Dies ist meiner Ansicht nach charakteristisch für ein Kontinuum.
Richards Paradoxie
In der Paradoxie nach Jules Richard (1862-1956) finden wir einen ähnlichen Aufbau wie in Cantors Diagonalargument. Es wird eine Liste E aller Dezimalzahlen, die mittels einer endlichen Anzahl an Worten (Ziffern) definiert werden können, als gegeben angenommen. Da man sich diese Liste von Zahlen geordnet vorstellen kann, wird die Konstruktion einer Zahl N, die nicht in der Liste vorhanden ist, aber dennoch mittels einer endlichen Anzahl an Worten definiert wird, wie folgt beschrieben: „Wenn die n-te Ziffer in der n-ten Dezimalzahl p ist, sei in N die n-te Ziffer p+1 (oder 0 wenn p=9). Dann ist N verschieden von allen Elementen von E;“ (S. 57 Fußnote 100)1. Da aber N den Kriterien für die Zahlen in E entspricht, gehört sie zu E, obwohl E zuvor als vollständige Liste betrachtet wurde.
Um zu verstehen, was hier „alle Elemente“ meint, müssen wir genau betrachten, wie E definiert, bzw. ob sie endlich oder unendlich ist. Im Falle einer endlichen Liste kann der Begriff alle die Elemente der Liste präzise umfassen. Konstruieren wir nach dem angegebenen Verfahren aus dieser Liste eine neue Zahl, so kann diese definitionsgemäß nicht zur zuvor aufgestellten Liste gehören. Dies jedoch ist keine Antinomie, sondern eine Konsequenz aus einer eindeutigen Listendefinition. Für die Definition einer endlichen Liste ist das vorliegende Kriterium „Dezimalzahl, die mittels einer endlichen Anzahl an Worten definiert werden kann“ unzureichend, da es keine endliche Auswahl aus dem unendlichen Zahlenvorrat ermöglicht.
Im Falle einer unendlichen Liste vermag der Begriff alle die Elemente der Liste nicht präzise zu bezeichnen, denn einer unendlichen Liste kann definitionsgemäß stets neue Elemente hinzugefügt werden. Folglich muss die Voraussetzung der Vollständigkeit der Liste (sprich: alle Dezimalzahlen, die mittels einer endlichen Anzahl von Worten definiert werden können) als falsch betrachtet werden. Ein Argument, das schon gegen die Voraussetzungen des Diagonalarguments vorgebracht wurde. Dies zeigt, dass die widersprüchlichen Folgerungen dieser Paradoxie aus der lückenhaften, d. h. ohne hinreichende Kriterien aufgestellten Definition von E entspringen. Anbei: Eine vollständige unendliche Liste aller Dezimalzahlen, welche durch Richards Verfahren um weitere Zahlen ergänzt werden könnte, wäre im Sinne Cantors ein Beweis für die Nichtabzählbarkeit der Menge der Dezimalzahlen.
Schluss
Ich bin der Ansicht, dass die Darstellung der Begriffskonstruktionen und die Analyse der Antinomien gezeigt haben, dass die Widersprüche keine Folgerungen aus widerspruchsfreien Prämissen (bzw. Axiomen) sein können, sondern auf Widersprüchlichkeiten, Doppeldeutigkeiten und Unzulänglichkeiten in der logischen Grundkonstruktion zurückzuführen sind. Daraufhin verweist zumindest die Argumentation von Domeisen, in der meiner Einschätzung nach die möglichen Einwände behandelt und widerlegt wurden. „Ich bestreite, dass die Paradoxien ein Problem der Logik sind; sie stehen vielmehr im Widerspruch zur Logik.“ (S. 23)1 Die Versuche, Antinomien aus der Logik zu entfernen, erscheinen mir gleichermaßen Versuche zu sein, die Konzeption der Logik weiterzuentwickeln. Und dazu besteht berechtigter Anlass, denn welchen Nutzen kann man sich von der Befestigung antinomischer Strukturen in der Logik versprechen?
Literatur
1 Domeisen, Norbert „Logik der Antinomien“, Peter Lang Verlag, Bern 1990
2 Thiel, Christian „Philosophie und Mathematik“, Wissenschaftliche Buchgesellschaft, 1995 Darmstadt